Symetrické kryptosystémy nehledíc na množství předností, mají jeden velký nedostatek. Je spojený se situací, kdy vzájemnou komunikaci mezi sebou provádí ne tři, čtyři osoby, ale stovky a tisíce lidí. V tomto případě je nutné, pro každý pár, který si vzájemně dopisuje, vytvořit svůj tajný symetrický klíč. Což ve výsledku přivádí k existenci v systému N uživatelů N2/2 klíčů. A to už je velmi "slušné" číslo. Kromě toho, při porušení důvěrnosti kteroukoliv pracovní stanicí, získá záškodník přístup ke všem klíčům tohoto uživatele a může odesílat, jakoby jeho jménem, zprávy všem abonentům s kterými si "oběť" dopisovala.
Svérázným řešením tohoto problému bylo objevení se asymetrické kryptografie. Asymetrická kryptografie byla od začátku pojata jako prostředek předání zpráv od jednoho objektu druhému (a ne pro důvěrnou archivaci informací, která je zajištěna pouze symetrickými algoritmy). Základní myšlenka asymetrických kryptoalgoritmů je v tom, že pro šifrování zprávy se používá jeden klíč a pro dešifrování – jiný.



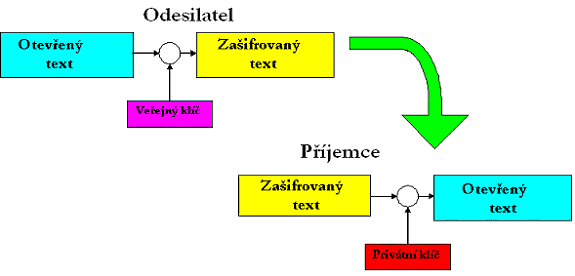
Kromě toho je procedura šifrování zvolena tak, aby byla nevratná i se známým šifrovacím klíčem – to je druhá nutná podmínka asymetrické kryptografie. To znamená, že se znalostí šifrovacího klíče a zašifrovaného textu je nemožné obnovit původní zprávu – je možné jej přečíst pouze s pomocí druhého klíče – dešifrovacího klíče. A jestliže je to tak, je možné šifrovací klíč pro odesílání dopisů jakékoliv osobě vůbec neskrývat – vědouc, že je stejně nemožné přečíst zašifrovanou zprávu. Proto se šifrovací klíč v asymetrických systémech nazývá "otevřeným klíčem“ a dešifrovací klíč musí příjemce zpráv uchovávat v tajnosti – nazývá se "zavřeným klíčem". Vnucuje se otázka: "Proč, když známe otevřený klíč nelze vypočítat zavřený klíč?" – toto je třetí nutná podmínka asymetrické kryptografie – algoritmy šifrování a dešifrování se vytvářejí tak, aby bylo, znaje otevřený klíč, nemožné vypočítat zavřený klíč. Takže do základů zařízení asymetrických krypto systémů je položen pojem jednostranné funkce. Existuje několik dobře známých asymetrických kryptosystémů: RSA, ElGamal, Rabin.
Asymetrická kryptografie učinila ještě dostatečně významný průlom v technologii primárního šíření klíčů. Jestliže byla pro symetrické kryptosystémy povinná předběžná výměna na uzavřeném kanálu (obvykle osobně z ruky do ruky), tak nyní se pro to objevily úplně nové způsoby.
Metoda Diffi-Hellmana používá algoritmus podobný algoritmu RSA, pro prvotní výměnu klíčů v symetrických krypto systémech na otevřeném kanálu, ale jen v takovém, kde je nemožná falzifikace zpráv. Tato metoda je podmíněna obtížností řešení úlohy diskrétního logaritmování.
Algoritmus RSA je klasikou asymetrické kryptografie. Používá se v něm pro odesílání zpráv nevratná transformace s velkou mocninou celých čísel podle modulu.
Jak se ukázalo, asymetrická transformace umožňuje velmi hezky řešit i úlohu autenticity autora zprávy – jednoduchou změnou pořadí použití otevřeného a zavřeného klíče.
Prakticky pro každý kryptoodolný algoritmus nebo protokol může být ukázáno, že v převážné většině případů (a se správným výběrem parametrů) se útok svádí na řešení určité obtížné úlohy, například rozložení na násobky (faktorizace) velkého složeného čísla. Přitom nebyla z hlediska existence dokázána optimální výpočetní složitost algoritmu řešení úlohy pro náhodně vybrané parametry.