Pracují s bloky otevřeného textu nebo šifrovaného textu – obvykle o délce 64 bitů nebo delší. Výchozí otevřená zpráva se rozbíjí na bloky – odřezky s fixovanou délkou, šifrování se uskutečňuje způsobem použití tabulky záměny (závislé na klíči, ale ne na čísle bloku) bloku za blok. Bloková šifra používající jeden a týž klíč vždy při šifrování transformuje jeden a týž blok otevřeného textu do jednoho a téhož šifrovaného textu. Výsledek šifrování záleží na všech výchozích bajtech tohoto bloku. Schéma se používá při paketovém přenosu informací a šifrování fajlů.

V závislosti na charakteru aplikací prováděných s daty se algoritmy dělí na:

• Přestavující.
  Bloky informací (bajty, bity, větší jednotky) se sami od sebe nemění, ale mění se pořadí jejich postupu, což dělá informaci nedostupnou pro postranního pozorovatele.
• Substituční.
  Samotné bloky informací se mění podle zákonů kryptoalgoritmu. Převážná většina současných algoritmů patří do této skupiny.

Všimněte si: jakékoliv kryptografické transformace nezvětšují objem informace, ale pouze mění její znázornění. Proto, jestliže program šifrování významně (více než o délku titulku) zvětšuje objem výstupního fajlu, tak je jeho základem neoptimální a možná vůbec nekorektní kryptoalgoritmus. Zmenšení objemu zakódovaného fajlu je možné pouze za přítomnosti zabudovaného algoritmu archivace v kryptosystému a za podmínky komprese informace.

Substituční a Přestavující šifry.

Než se objevily počítače tak se kryptografie sestávala z algoritmů na symbolickém základu. Různé kryptoalgoritmy buď nahrazovaly jedny symboly jinými nebo substituovaly symboly. Lepší algoritmy dělaly jedno i druhé a to opakovaně.
Dnes je vše značně složitější, ale filozofie zůstává stejná. První změna spočívá v tom, že algoritmy začaly pracovat s bity a ne se symboly. Je to důležité alespoň z hlediska velikosti abecedy - z 26 elementů do 2. Většina dobrých kryptografických algoritmů dodnes kombinuje substituce a přestavení.

Substituční šifry.
Substituční šifrou nazýváme šifru u které se každý symbol otevřeného textu v šifrovaném textu nahrazuje jiným symbolem. Příjemce invertuje substituci šifrovaného textu a obnovuje otevřený text.
V klasické kryptografii existují 4 typy substitučních šifer:

1. Jednoduchá substituční šifra neboli monoabecední šifra - je to šifra, která každý symbol otevřeného textu nahrazuje odpovídajícím symbolem šifrovaného textu. Jednoduchými substitučními šiframi jsou kryptogramy v novinách. Jednoduché substituční šifry se lehce otevírají, protože šifra netají frekvenci používání různých symbolů v otevřeném textu.
2. Jednozvučná (homofonická) substituční šifra je podobná na jednoduchý substituční kryptosystém kromě toho, že jeden symbol otevřeného textu se zobrazuje na několik symbolů šifrovaného textu. Například “?” může odpovídat 5,13,25 nebo 56, “?”- 7,19,31 nebo 42 atd. Jsou složitější pro otevření než jednoduché substituční šifry, i když neskrývají všechny statistické vlastnosti jazyku otevřeného textu. Za pomoci otevření známým otevřeným textem se tyto šifry triviálně otevírají. Otevření za pomoci pouze šifrovaného textu je složitější, ale zabírá v počítači pouze několik vteřin.
3. Polygramová substituční šifra – je to šifra, která bloky symbolů šifruje podle skupin. Například “???” může odpovídat “RTQ”, “ABB” může odpovídat “SLL” atd.
4. Polyabecední substituční šifra se sestává z několika jednoduchých substitučních šifer. Například může být použito pět jednoduchých substitučních šifer; každý symbol otevřeného textu se nahrazuje s použitím jedné konkrétní šifry. V polyabecedních substitučních šifrách jsou množstevní jednopísmenné klíče, každý z nich se používá pro šifrování jednoho symbolu otevřeného textu. Prvním klíčem se šifruje první symbol, druhým klíčem – druhý symbol atd. Po použití všech klíčů se cyklicky opakují. Jestliže se používá 20 jednopísmenných klíčů, tak se každé 20 písmeno šifruje stejným klíčem. Tento parametr se nazývá periodou šifry. V klasické kryptografii se šifry s dlouhou periodou otevíraly obtížněji než s krátkou periodou. Použití počítačů umožňuje lehce odhalit substituční šifry s velmi dlouhou periodou.
Znamenitá Caesarova šifra, ve které se každý symbol otevřeného textu nahrazuje symbolem nacházejícím se o tři symboly napravo podle modulu 26 (“A” se nahrazuje za “D”, “B”-za “E”,…,”Y”-za “B”, “Z”- za“C”), představuje jednoduchou substituční šifru. Je opravdu velmi prostá, protože abeceda šifrovaného textu představuje posunutou a ne náhodně rozdělenou abecedu otevřeného textu.


Přestavující šifry.
V substituční šifře není otevřený text, ale řada symbolů. V jednoduché sloupcové substituční šifře se otevřený text píše horizontálně na diagramovém listu papíru o fixované šířce a šifrovaný text se odečítá na vertikále. Dešifrování je záznam šifrovaného textu vertikálně na diagramovém listu papíru o fixované šířce a poté se odečítá otevřený text horizontálně.

Otevřený text: COMPUTER GRAPHICS MAY BE SLOW BUT AT LEAST IT’S EXPENSIVE

COMPUTERGR
APHICSMAYB
ESLOWBUTAT
LEASTITSEX
PENSIVE

Šifrovaný text: CAELP OPSEE MHLAN PIOSS UCWTI TSBIV EMUTE RATS GYAE RBTX

Schéma práce blokové šifry je možné popsat funkcemi Z=EnCrypt(X,Key) a X=DeCrypt(Z,Key)

Klíč Key je parametrem blokového kryptoalgoritmu a představuje jistý blok dvojkové informace o fixované velikosti. Výchozí (X) a zašifrovaný (Z) blok dat mají také fixovanou bitovost, stejnou mezi sebou, ale nemusí odpovídat délce klíče.
Blokové šifry jsou základem, na kterém se realizují prakticky všechny kryptosystémy. Metodika vytvoření řetězců ze zašifrovaných blokovými algoritmy bajtů umožňuje šifrovat pakety informací neomezené délky. Taková vlastnost blokových šifer, jako rychlost práce, se používá asymetrickými kryptoalgoritmy, které jsou sami o sobě pomalé. Nepřítomnost statistické korelace mezi bity výstupního toku blokové šifry se použije pro výpočet kontrolních součtů paketů dat a v hašování hesel.


Funkce stabilní blokové šifry Z=EnCrypt(X,Key) musí odpovídat těmto podmínkám:

• 1. Funkce EnCrypt musí být vratnou.
• 2. Nesmí existovat jiné metody přečtení zprávy X podle známého bloku Z, kromě jak úplným přebráním klíčů Key.
• 3. Nesmí existovat jiné metody určení, jakým klíčem Key byla uskutečněna transformace známé zprávy X na zprávu Z, kromě jak úplným přebráním klíčů.

V blokovém algoritmu s textem se provádí podle určitého schématu následující operace (nalevo jsou dány podmíněná označení těchto operací grafických schémat algoritmů):









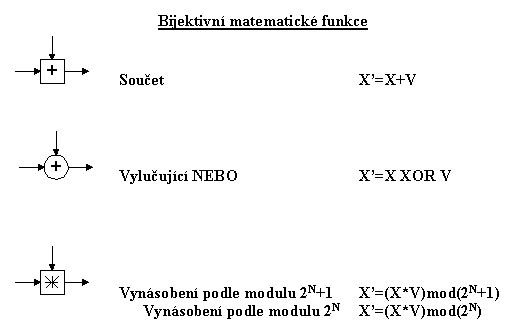
Jako parametr V pro jakoukoliv transformaci se může použít:

• fixované číslo (například X'=X+125),
• číslo získané z klíče (například X'=X+F(Key)),
• číslo získané z nezávislé části bloku (například X2'=X2+F(X1)).

Poslední varianta se používá v schématu nazvaném jménem jejího zakladatele Feistelova síť (něm. Feistel).

Feistelova síť je další modifikací výše popsané metody směšování průběžné části šifrovaného bloku s výsledkem jisté funkce vypočítané z jiné nezávislé části stejného bloku. Tato metoda získala široké rozšíření, protože zabezpečuje plnění požadavků o opakovaném použití klíče a materiálu výchozího bloku informací. Klasická Feinstelova síť má následující strukturu:


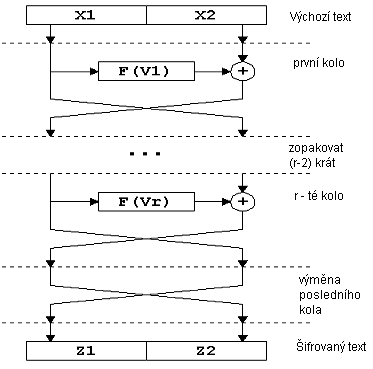
Obr.8.Síť Feistela.

Nezávislé toky informací vyvolané z původního bloku se nazývají větvemi sítě. V klasickém schématu jsou dvě. Veličiny Vi se nazývají parametry sítě, obvykle jsou to funkce z materiálu klíče. Funkce F se nazývá tvořící. Činnost sestávající se z jednorázového výpočtu tvořící funkce a následující přiložení výsledku na jinou větev s výměnou míst se nazývá cyklem nebo kolem (angl. round) Feistelovy sítě. Optimální počet cyklů K - od 8 do 32. Důležité je, že zvýšení počtu cyklů významně posiluje kryptoodolnost jakékoliv blokové šifry vůči kryptoanalýze. Je možné, že tato zvláštnost měla vliv na tak aktivní rozšíření Feistelovy sítě – vždyť při nalezení řekněme nějakého slabého místa v algoritmu je prakticky vždy dostatečné zvýšit počet cyklů na 4-8, bez přepisování samotného algoritmu. Často vývojáři algoritmu nefixují počet cyklů, ale pouze uvádějí rozumné limity (povinně spodní a ne vždy horní) tohoto parametru.
Okamžitě vzniká otázka – zda je toto schéma vratné? Je zřejmé, že ano. Feistelova síť má vlastnost, že jestliže je dokonce jako tvořící funkce F použita nevratná transformace, tak i v tomto případě bude celý řetězec obnoven. Dochází k tomu v důsledku toho, že pro zpětnou transformaci v Feistelově síti není třeba vypočítávat funkci F-1.

Režimy práce blokových šifer.
V procesu šifrování je aktuální takový problém, jako je délka dat, nerovných délce 1 bloku kryptoalgoritmu. Pro řešení těchto problémů byly zavedeny do kryptosystému algoritmy vytváření řetězců (angl. chaining modes). Nejčastěji se v praxi setkáváme s těmito režimy:

• elektronická kódovací kniha - ECB (Electronic Code Book);
• řetězení bloků šifrovaného textu - CBC (Cipher Block Chaining);
• zpětná vazba šifrovaného textu - CFB (Cipher Feed Back);
• zpětná vazba na výstupu - OFB (Output Feed Back);

Přednostmi blokových šifer jsou:
1. Odolnost vůči opakovanému použití jednoho a téhož klíče, a to i za přítomnosti prakticky neomezeného počtu párů otevření – šifrovaný text, získaných na jednom klíči;
2. Libovolnost přístupu k šifrovanému textu (s přesností na blok).
3. Možnost realizace na základě blokové šifry, gamovací šifra.

K nedostatkům patří:
1. Koeficient rozmnožení chyby je rovný délce bloku. Jednotlivá chyba v šifrovaném textu vyvolává zkreslení asi poloviny otevřeného textu při dešifrování. Toto vyžaduje použití výkonných kódů, které opravují chyby.
2. Blokovost šifrování. Ze dvou stejných bloků otevřeného textu vycházejí stejné bloky šifrovaného textu.
3. Významně nízká rychlost práce ve srovnání s gamováním (pro kvalitní šifry), podmíněnou složitostí realizace algoritmu jednoduché záměny v abecedách o velké kapacitě, protože je zřejmé, že pro dostatečné zabezpečení odolnosti délky bloku je tabulkové zadání takové operace nemožné.
4. Vysoká složitost realizace operací standardně používaných při vytváření blokové šifry, jakož i operace posunu, vyčlenění částí bloků v šifrovaném bloku atd.
5. Relativně velký objem paměti vyžadovaný pro archivaci vnitřních dat (zejména tabulek záměny pro rozptylovací transformace) používaných při šifrování.

Nejkritičtějším parametrem blokových šifer je rychlost šifrování, která může být nižší než u gamovací šifry až o několik desetinásobků. Nicméně možnost libovolného přístupu k jednotlivým částem zprávy a odolnost vůči opakovanému použití klíčů dělají tyto algoritmy přitažlivými pro použití jako standardu při ochraně informací.
Útoky na blokové šifry je možné realizovat s pomocí diferenciální kryptoanalýzy, kam patří také diferenciální analýzy na základě odmítnutí zařízení, lineární kryptoanalýzy, silového útoku na základě rozdělených výpočtů.